Note:: This is an archive post from 2013 and octree construction is used for NNS.
Octree is a type of data-structure especially used for particle tracking in CFD(computational fluid dynamics) and also for the nearest neighbor search. It is also a space partition method which is similar to binary tree but having eight children, means each internal node of an octree have eight children. The general meaning of octree is oct + tree, which means a given cube is divided into eight smaller cube. The division is shown below

Fig: Octree Visualization
Construction of octree in brief
- The space containing all the particles (say millions) are enclose within a cube
- The length and side of cube are determined by the minimum (Xmin, Ymin, Zmin) value and maximum (Xmax, Ymax, Zmax) value of coordinate of distribution of particles.
- Now, the parent cube is divided into eight smaller cube of length l/2 of parent cube, where l is the length of parent cube.
- A coordinate of new cube is obtained from the parent cube with certain mathematical calculation on it’s side (l).
- The cube is further divided recursive if the parent cube contain more than one particle in it.
- The depth of division of cube is predefined or can be divided until a single particle is enclosed within a child cube.
- The track of each particle is kept, let’s say we have particle P(x, y, z) shown in above figure of cube, for the particular of value x, y and z, the particle P lies on the cube at m9, m10, m11, m14, m16, V7, m17, m19.
- Similarly the track of co-ordinate of STL triangle (it is a triangular representation of 3d data) is kept, i.e. the vertex v1 of triangle P lies on some of the cube.
The mathematical recursive formula for construction of octree
Let’s us assume the name of eight cubes which is constructed form the internal parent cube be
left_top_front, left_top_back, left_down_front, left_down_back, right_top_front, right_top_back,
right_down_front, right_down_back.
Suppose the length of the parent cube is “l” and the cube with its vertex are taken from the above figure.
Below case if for the cube being at the origin but for the actual practice Xmix, Ymin , Zmin is added to the origin.
Now the minimum and maximum coordinate of the child cube can be obtain as follow
left_top_front = (m6, m5) = ((0, l/2, 0), (l/2.l, l/2))
left_top_back = (m13, m3) = ((0, l/2, l/2), (l/2.l, l))
left_down_front = (V4, m14) = ((0, 0, 0), (l/2.l/2, l/2))
left_down_back = (m18, m11) = ((0, 0, l/2), (l/2.l/2, l))
right_top_front = (m7, m2) = ((l/2, l/2, 0), (l.l, l/2))
right_top_back = (m14, m6) = ((l/2, l/2, l/2), (l. l, l))
right_down_front = (m15, m9) = ((l/2, 0, 0), (l, l/2, l/2))
right_down_back = (m19, m10) = ((l/2, 0, l/2), (l, l/2, l))
Thus, using above formula the octree can be constructed recursively.
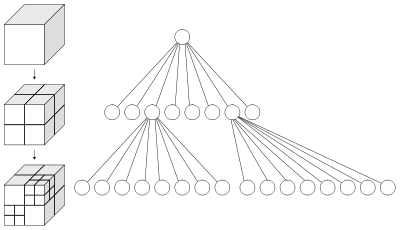
Fig: Octree parent-child, © Wikipedia
NNS using octree
- First of all the sample point is taken say P(x, y, z).
- Now the cube containing this sample point is found out by traversing the tree using BFS.
- After the cube is found out, the other cube nearer to its surface and edge are found out traversing the tree again.
- Since each cube in an octree contain certain particles so all the particles lying to the nearer cube is found out and placed in certain data structure.
- Fnally, the distance between the candidate particle and all the other search particle is found out so that to discover the nearest distance and eventually the nearest particle.